Eric Trager has a new article out for the Washington Institute for Near East Policy.

I genuinely appreciate the research Trager does, though I often disagree with his analysis, but I wanted to highlight a major problem I read in his article:

The official election bylaws have yet to be released, but reports suggest that the party-list elections will be based on district-wide voting, with winners determined using the “largest remainder system.” According to this method, only those parties that meet or exceed the quota of votes for a given district will be able to win seats. For example, in a district with five seats, a party must win at least 20 percent of the vote to gain a seat; even if a party finishes within the top five, none of its candidates will be seated if it does not cross the 20 percent threshold.

If this system is enacted, it will significantly hamper newer parties in the next parliamentary elections. The local nature of these party-list elections — as opposed to the nationwide systems in other democracies — makes it unlikely that small and still-forming parties will be able to compete effectively. Even in those districts where they might field multiple candidates, they would have trouble surpassing the relatively high thresholds that the largest remainder system implies.

This is simply untrue about largest remainder systems; largest remainders do not make it necessary to reach a quota.  This should be somewhat intuitive if you think about.  If this were really the case, then what if many parties ran and nobody reached that number?  All PR systems, broadly speaking, rely on quotas to allocate seats; the largest remainder system is not exceptional.  In fact, it is actually more favorable to smaller parties than the highest average method.  To illustrate this, lets compare several scenarios using three different methods.  The first is the standard highest average method of allocation seats, the D’hondt method.  For the largest remainder system, we will use a Droop quota as examples.  For each example, I’ll have one party receive 60,000 votes (60% in our district), while the next two only get 20,000 and 10,000 respectively.  The other parties only get 1,000 each.  This is an extremely fractured party system, but it will help demonstrate what could happen in many Egyptian districts.

In the D’Hondt method, the total votes cast for every party (100,000) is divided, first by 1, then by 2, then 3,  up to the total number of seats to be allocated (six for our example).  Then the N highest entries (six in our example) are counted and awarded to those parties.

So in this example, Party A wins five seats, while Party B wins one.

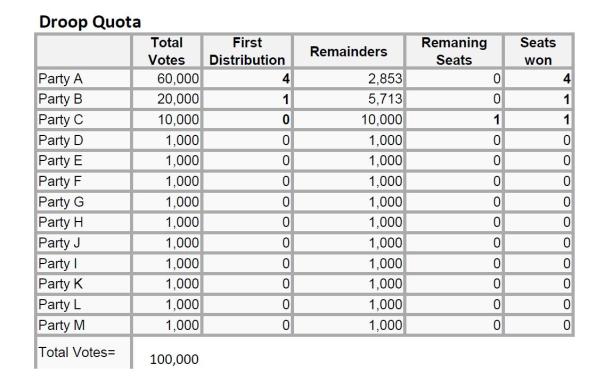
Largest remaineder methods, however, work a bit differently.  Instead, total votes are divided by N seats to create a quota used for allocation.  Parties are awarded seats for every time they reach that quota.  However, after the quota is reached a certain number of times, there are bound to be remainders.  The remainders are then used to determine who will get the remaining seats.  So using a Droop quota below, we can use the same election scenario and see how things would play out.

First the Droop quota is calculated (100,000/(N+1))+1, which equals 14,286.  This is the number of votes a party needs to get one seat in the first distribution. After this, however, we still have one more seat to allocate.  Party C has only 10,000 votes, much less than the Droop quota, but they have the largest remainder votes after their initial tally was divided by the quota.  Because of this, they get the remaining seat, which makes this a more equal allocation method than highest averages.